ELECTRIC OPRPHEUS ACADEMY
SPILLING THE BEANS #17 WAVESHAPING
distortion
Der Terminus 'wave shaping' geht angeblich auf J.C.Risset zurück
und wird als 'nichtlineare Verzerrung' beschrieben. Schön und gut
- aber was wäre denn 'lineare Verzerrung' ? Ganz einfach: eine Lautstärkeänderung,
ein 'scaling', ein 'gain'. Alles andere ist Amplitudenverzerrung.
Klar, wenn ich ein bestimmte Wellenform über einen Verzerrer schicke,
kommt eine typisch andere, deformierte Wellenform heraus. In den wenigsten
Fällen ist die resultierende Wellenform pegelunabhängig. Ich
würde daher vorschlagen diese Methode einfach Verzerrung (distortion)
zu nennen und uns den Begriff 'wave shaping' für andere Ansätze
aufbewahren.
In VASP und AMP gibt es eine Sammlung von ungefähr 40 Arten von Verzerrung:
umkehrbahre, nicht umkehrbare, Sättigungen, Spiegelungen, modulative,
nach Standardfunktionen, nach Sonderfunktionen ....
Sie alle zeichnen sich durch eine typische Amplitudenkennlinie aus, die
in den meisten Fällen je nach gain anders ausschaut. Diese Kennlinie
zeigt an, welche Amplitude herauskommt, wenn man eine bestimmte Amplitude
hineinschickt.
Ich versuche hier eine Sytematik der Verzerrungstypen.
signed power
Ich beginne mit der fundamentalsten, 'signed power', eine Potenzierung
der Amplitude unter Beibehaltung des Vorzeichens (positive bleiben positiv,
negative negativ).
±Aneu = ±Ax
wobei x ein beliebiger Faktor (Exponent) sein kann. Ist der Faktor >1,
haben wir es mit Potenzen zu tun; ist er <1, mit Wurzeln; ist er genau
=1, bleibt die Amplitude unverändert.
Dieser Verzerrungstyp, dist.spow in VASP und AMP, hat
zwei bedeutende Eigenschaften: Erstens ist er reversibel. dist.spow
2 kann durch dist.spow 0.5 exakt rückgängig
gemacht werden. Diese Umkehrbarkeit findet man bei anderen Typen mehr
oder weniger auch. Einzigartig ist, dass die Art der Verzerrung pegel-unabhängig
ist. Egal, auf welchem Pegel sie angewendet wird: die resultierenden Pegelveränderungen
insgesamt können drastisch sein, die Verzerrung ist immer dieselbe.
Das sind tyische Kennlinen davon. (Man muss sie sich in beiden Richtungen
fortgesetzt denken, rechts oben für Amplituden >1, links unten
gespiegelt für negative Amplituden):
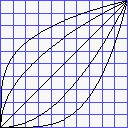
Kennlinien, nicht Wellenformen. Wendet man sie auf einen Sinuston (mit
Amplitude 1) an, ergeben sich folgende Wellenformen:
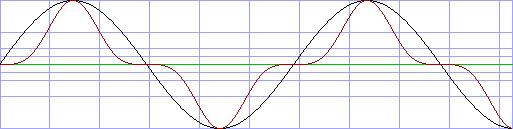
schwarz: sinus, rot: dist.spow 4
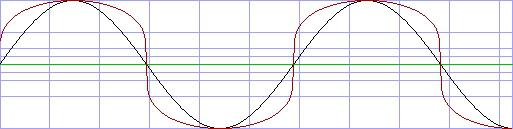
rot: dist.spow 0.25
Diesen Verzerrertypus verwendete ich sytematisch bei meiner Arbeit an
ATEM (Werke 3, ccr403). Ich benutzte dazu einen 'Quadrierer', ein modifizierter
Ringmodulator, und einen 'Radizierer', ein Analogrechenbauteil (beides
Einzelstücke, Sonderanfertigungen von Georg Danczul). In
diesem Stück sind die Verzerrungsgrade ein wichtiger Teil der Komposition.
[Wir besorgten uns die hochpräzisen Analogrechenbauteile als
Warenmuster, den einzeln zu kaufen gab es die nicht. Georg ging in seinem
Perfektionismus soweit, dass er die Platinen im Backofen 'künstlich
altern' liess, damit sie stabiler wurden]
Eine kurze Abschweifung: dbx
Eines der ersten noise-reduction Syteme für Tonbänder von dbx
verwendete solche Funktionen, allerdings auf Hüllkurvenebene. Das
aufzunehmende Signal wurde durch einen Radizierer codiert und bei der
Wiedergabe durch einen Quadrierer entcodiert. Angenommen ein Signal hätte
maximal -60db, dann wurde es durch die Codierung auf -30db angehoben.
Dazu kam dann das unvermeidliche Bandrauschen von ca. -70db. Bei der Entcodierung
erhielt das Signal wieder seine ursprünglichen -60db, das Bandrauschen,
an den ruhigen Stellen, -140db. (Abgekürzt erklärt! Natürlich
war da noch eine Menge Elektronik drin, vor allem Korrekturfilterungen,
etc.)
[Ich hatte dbx für alle Bandmaschinen: 8-kanal, 4-kanal, stereo
- und war von Anfang an begeistert über diese, nie dagewesene Dynamik.
Was man damals allerdings nicht wusste: Solcherart codierte Tonbänder
sind nur schwer lagerbar, der Magentismus verändert sich über
lange Zeiträume und dann hört man das Bandrauschen als 'Pumpen'
(breathing). Nichtsdestowenig liess sich das Gerät, bei Umgehung
der Korrekturfilter, auch als Kompressor und Expander einsetzen.]
Ein Hüllkurven-Kompressor/Expander nach solchen Funktionen ist
in VASP als boost verfügbar, in der Zeitebene wie
auch im Spektrum.
Sättigungen
Sättigung (saturation) nennt man ein Amplitudenverhalten, bei dem
die Amplitude über einen Grenzwert nicht hinauskommt. Im Gegensatz
zum digitalen Limit, gibt es hier aber keinen Knick (wie der digitale
Plafond), sondern die Kennlinie nähert sich asymptotisch dem Grenzwert.
[Man kennt das von den Tonbändern. Deren Charakteristik ist weitgehend
linear, über einer bestimmten Amplitude beginnen sie zu verzerren.
Es war durchaus ein Stilmittel, die Aufnahme etwas in die Sättigung
zu treiben, wodurch der Klang etwas verzerrt, aber eben tatsächlich
'satter' wurde.]
Kleine Amplituden bleiben praktisch unverändert, grössere werden
in Richtung Limit verzerrt. In der Sammlung von VASP und AMP sind drei
Varianten verfügbar:
dist.hsat hyperbolische Sättiung
dist.tsat tangentiale Sättigung
dist.erf nach einer komplizierten
Funktion 'error function'
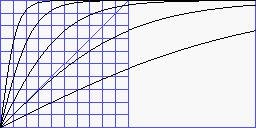 dist.hsat |
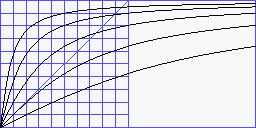 dist.tsat |
Ganz besonders die hyperbolische Sättigung kann ich wärmstens
empfehlen. Für Material mit diffusem Spektrum (wo es mehr um Impuls
als um Tonhöhen geht), leistet sie wahre Wunder: Harte Attacks, Explosionen,
Schüsse, Blitz und Donner ...
Im Gegensatz zu Limitern, die mit der Pegelbegrenzung auch die Energie
reduzieren, geht dabei die Energie in die Verzerrung und somit nicht verloren.
Beim CD-Mastern hab ich die Funktion immer wieder verwendet, zum Beispiel
der Böllerschuss in AINT' THERE TV (ccr302).
Hinweisen möchte ich auch auf die Umkehrfunktion dist.hsat.
Sie ist nicht einfach zu handhaben. Wenn man Glück hat, kann man damit aber Übersteuerungen von Aufnahmen auf Tonband oder Cassette
korrigieren.
Spiegelungen
Spiegelnde Verzerrungen nenne ich solche, bei denen die Amplitude ab einem
bestimmten Scheitelwert wieder zurückgenommen wird. Die klassischen
Gitarreverzerrer sind von dem Typ. In VASP sind zwei davon digital nachgestellt:
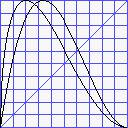
dist.fuzz0, .fuzz1
Die Amplitude geht nach dem Grenzwert wieder gegen 0 (und bleibt darüberhinaus
0). Da aber auch die Wellen extrem hoher Pegel immer wieder durch den
Scheitelpunkt müssen, bleibt der Pegel darüber stets vollausgesteuert,
lediglich die Verzerrung ändert sich. Man kennt das von den verzerrten
Gitarrentönen, die lange auf einem Pegel gleichsam stehenbleiben,
bevor sie verklingen
[Es wäre eine eigne Untersuchung wert, wie solche Verzerrer
die Harmonik der Rockmusik beeinflusst haben: weg von den Dreiklängen,
hin zur Quartenharmonik ...]
Es findet sich noch ein Dutzend weiterer spiegelnder Verzerrungen in VASP
(siehe Manual). Sie sind nicht umkehrbar.
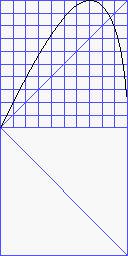
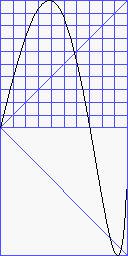
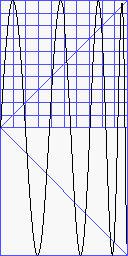
Modulierende Verzerrungen
So nenne ich Verzerrungen, die über einem bestimmten Pegel zu oszillieren
beginnen und somit Modulation ins Spiel bringen. Sie sind weder pegelunabhängig
noch umkehrbar. Dazu gehört dist.cproj (circular
projection), eine der energiereichsten Verzerrungen, die ich kenne. Ich
verwendete sie gelegentlich für tiefe Ausklänge, zum Beispiel
in meiner umstrittenen Neuvertonung von Barockarien BELCANTO.
 |
 |
 |
Ähnlich, aber subtiler, ist die Cosinus-Automodulation dist.cosmod
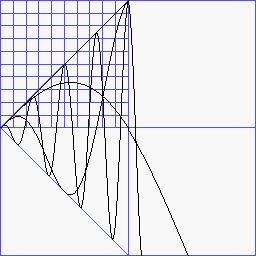
Verzerrungsgrade 0 (linear),1,4,8
Katharina Klement verwendete sie in ihren 13 MINIATUREN (Miniatur
12, KALK 01) mit Klavierakkorden.
Nicht so drastisch, aber auch modulierend sind Kennlinien nach einigen
Sonderfunktionen, wie Fresnel-, oder Sinusintegral.
|
|
|
Für letztere würde die Veränderung der Wellenform so
aussehen:
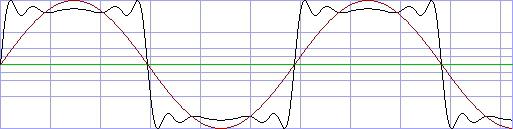
(rot: Sinuston, schwarz: Verzerrung durch dist.sinint)
Das VASP-script dazu:
gen.sin 150hz
dist.sinint 8
Selbstverständlich ist Verzerrung auf alles anwendbar, nicht bloss
auf Sinustöne, und erzeugt dann die typischen Kombinationstöne;
in diesem Fall auch Modulationen durch das Überschwingen bei grösseren
Amplituden.
In VASP können diese Verzerrungen auf den linken und rechten Kanal
getrennt angewendet werden, auf den complexen Radius (rdist) sowie auf
die instantaneous frequency (fdist).
Frei definierbare Kennlinien
Wie man Wellenformen konstruieren kann, so könnte man auch Kennlinien
willkürlich konstruieren, oder zeichnen, oder aus einzelnen, nichtlinearen
Elementen zusammensetzen. Eine Konkordanz der Grafik mit den akustischen
Auswirkungen darf man aber nicht erwarten. Freilich kann man Kennlinien,
wie auch Wellenformen interpretieren lernen. Wie das wirklich klingt,
weiss man aber erst, wenn man es ausprobiert.
Anmerkung:
Alle hier vorgestellten Kennlinien sind symmetrisch hinsichtlich negativer
Amplituden. Das muss nicht so sein. Unter ubdist (unbalanced
distortion) findet man in VASP auch einige unsymmetrische, zu denen auch
die typische Verzerrung in Röhrengeräten gehört.
* * *
complexes wave shaping
Zum eigentlichen wave shaping gelangt man, wenn man von complexen Wellen
ausgeht.
Eine Sinusschwingung, als Kreisbewegung betrachtet, lässt sich durch
zwei Parameter beschreiben: die Amplitude (das ist der Radius der Kreisbewegung)
und die Frequenz (das ist die Geschwindigkeit der Kreisbewegung). Zusammen
bilden sie das, was man einen 'Phasor' nennt. In der Fachwelt nennt man
das auch 'instantaneous amplitude' und 'instantaneous frequency' - momentane
Amplitude und momentane Frequenz. Letzteres nicht ganz zu Unrecht, da
das bei einfachen Klängen (Sinustönen und langsam veränderlichen
sinusoidalen Tönen) tatsächlich dem entspricht, was wir als
Frequenz wahrnehmen. Bei Gemischen und beliebigen Klängen ist das
nicht mehr so einfach. In solchen Fällen ist der Phasor in jedem
Moment ein anderer. Dennoch ist das eine der wichtigsten Darstellungen
bei der Bearbeitung von Klangmaterial (ein 'Geheimtipp' sozusagen).
Andersherum:
Gesetzt der Fall, wir hätten einen hochpräzisen Sinusgenerator
mit zwei Steuereingängen, einen für Frequenz und einen für
Amplitude. Wir nehmen einen beliebigen Klang. Wie müssten die Steuerdaten
aussehen, damit der Generator exakt diesen, beliebigen Klang reproduziert
?
Die Antwort ist einfach: So einen Generator haben wir seit Jahrzehnten;
die Steuerdaten gewinnen wir durch eine Konvertierung eines complexen
Signales in besagte zwei Komponenten. In VASP ist das die Operation rdphi
(Konvertierung in Radius und Delta-Phase) und rdphi-
(Rückkonvertierung).
[Was man mit dieser rdphi-Darstellung alles machen kann, wird Thema
des heurigen Meisterkurses sein]
Durch die Analyse erhalten wir also die Steurdaten für Amplitude
und Frequenz. In der Resynthese wenden wir diese Steuerdaten auf einen
Sinusgenerator an. Die Analyse muss in jedem Fall complex erfolgen; für
die Resynthese können wir auch einen rein reellen Sinusgenerator
verwenden, wenn wir kein complexes Ergebnis brauchen.
Das Prinzip des wave shapings (manche nennen es wave shape synthesis)
beruht nun ganz einfach darauf, dass man für die Resynthese jede
beliebige andere Wellenform heranziehen kann, egal, ob reell oder complex.
Da gibt es zunächst die Standards, die man bereits von den Analog-Synthesizern
und Messgeneratoren kennt. (Ihre Benennung orientiert sich daran, welche
Wellenform man erhält, wenn das Ausgangssignal ein Sinus ist). In
VASP und AMP sind das:
|
waveshape.saw |
Sägezahn |
Die klassischen Wellenformen muss ich, glaube ich, nicht weiter erklären.
Dreieck und Rechteck gestatten auch eine kontinuierliche Einstellung des
Tastverhältnisses (duty pulse factor). Dazu kommt noch die Lemniskate,
bei der die Kreisbewegung des complexen Sinus durch eine Achterschleife
ersetzt wird. (Siehe: SPILLING THE BEANS #7 'Achterbahn').
Eine technische Anmerkung:
Bei der Resynthese durch runde Wellenformen gibt es nicht viele Probleme.
Bei kantigen (und das sind praktisch alle klassischen, vom Sägezahn
bis zum Nadelimpuls) schon ! Praktisch alle Wellenformen, deren Grundperiode
nicht ein ganzzahliges Vielfaches der digitalen Rasterung ist, geraten
unsauber - also ganz besonders höhere Grundfrequenzen. Das fängt
aber bei 400hz schon an !
Da hilft nur eines: oversampling. In VASP und AMP werden solche Wellenformen
daher standardmässig mit mindestens 4-fachem oversampling und entsprechender
Nachfilterung generiert.
register
Natürlich könnte man Wellenformen beliebig gestalten und tables
anlegen. Es läuft aber darauf hinaus, dass man Dutzende oder Hunderte
von samples oder Parameter händisch setzen muss.
Dem gegenüber empfehle ich eine Methode, bei der man Teiltöne
zusammenfasst. Ich nenne sie 'register', nach dem Vorbild eines Orgelregisters.
Dabei gibt es 3 Parameter: Der Anteil des Grundtones, der Anteil der geraden
Obertöne und der Anteil der ungeraden (ausser dem Grundton).
Grundlage davon ist wieder die, oben bereits erwähnte, Lemniskate
sowie zwei Ableitungen davon, die schärfere Spektren erzeugen.
|
register.lem |
Dreifache Registrierung nach Lemniskate |
(Solche dreiteiligen Register sind übrigens auch an mehreren Stellen
im Flötenmodell fmpipe eingebaut: für den eigentlichen
Ton, den Labialton und für das Grundgeräusch des Rohres).
Steuerdaten
Gehen wir einen Schritt weiter und machen uns frei von der Vorstellung,
dass man eine Wellenform durch eine andere ersetzen müsse. Sehen
wir die beiden analytischen Komponenten (momentane Amplitude und momentane
Kreisfrequenz) als reine Steuersignale, wie bereits eingangs beschrieben.
Was hindert uns daran, diese Steuersignale auf beliebige Parameter anzuwenden
? - Auch wenn es nur Parameter sind, die phänomenologisch Tonhöhencharakter
haben, sind die Möglichkeiten grenzenlos.
Dazu muss man die Steuerdaten eventuell etwas umformen.
[Auch das wird Thema des nächsten Meisterkurses werden.]
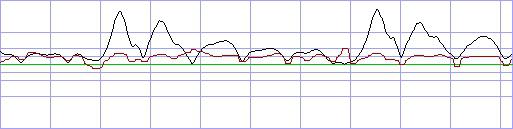
Sehen wir uns diese Daten einmal näher an. Hier der Ausschnitt eines
complex aufbereiteten Klanges:
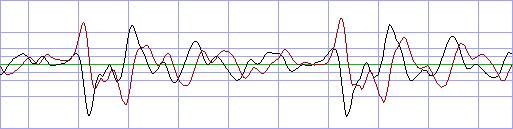
(xy-Darstellung, schwarz: Realteil, rot: Imaginärteil)
So sieht derselbe Ausschnitt nach der Konvertierung durch rdphi
aus:
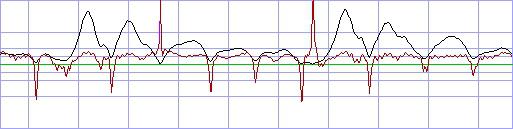
(rdphi-Darstellung, schwarz: Radius, rot: delta-Phase)
Der Radius ist klar: Er ist die Wurzel aus den Quadraten von Realteil
und Imaginärteil, die complexe Amplitude. Die Kreisfrequenz hat durchwegs
kleine, meist positive Werte mit gelegentlichen positiven und auch negativen
Spitzen (spikes).
Ihr Bereich liegt zwischen +pi und -pi. (Daher die Übersteuerung
in der Darstellung, deren Bereich zwischen +1 und -1 liegt).
Vergleicht man die spikes mit dem Radius, dann erkennt man auf einen Blick,
dass sie hauptsächlich dort auftreten, wo der Radius eine Senke zeigt
oder gegen 0 geht - also dort, wo die Bewegung in der x/y-Ebene knapp
am Nullpunkt vorbeigeht.
Derselbe Ausschnitt in der x/y-Ebene:
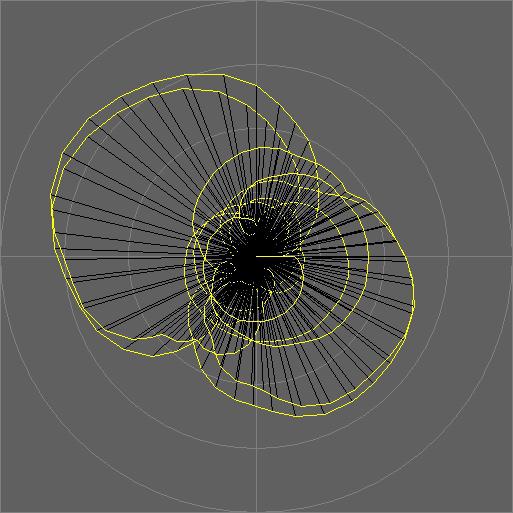
(x/y-Darstellung, waagrecht: Realteil, senkrecht: Imaginärteil)
An den äusseren Bögen sieht man sehr schön die Winkelgeschwindigkeit,
nämlich der Winkel von einem sample zum nächsten. Die schwarzen
Linien sind die Radien (complexen Amplituden) der samples. Im Zentrum
liegen diese Durchgangspunkte, an denen die Phase grössere Sprünge
macht, die sich in der delta-Phase als spikes zeigen. Für die Resynthese
darf man sie keinesfalls weglassen (das hätte ungewollte Verzerrungen
zur Folge), aber in Hinblick auf Steuerdaten sind sie nicht signifikant,
meistens sogar störend.
Es gibt mehrere Methoden, mit solchen spikes umzugehen. Eine klassische
ist die Anwendung eines Medianfilters. Derselbe Ausschnitt gefiltert:
Anmerkung:
So ein Medianfilter ist kein Filter im eigentliche Sinn. Seine hauptsächliche
Verwendung findet es in der Bildbearbeitung, wenn es darum geht, störende
einzelne Pixels zu eliminieren. Seine Wirkungsweise beruht darauf, dass
immer eine Gruppe benachbarter samples verglichen wird und das mittlere
daraus genommen. (Nicht der Mittelwert, dann wäre es nämlich
ein Tiefpassfilter - das mittlere, wenn man die Gruppe sortiert).
In diesem Fall war es median.y11 - nur im rechten Kanal
mit einer Breite von 11 samples. (Bei einer Mindestbreite von 3 könnte
man nur einzelne Nadelimpulse abfangen).
aperiodische Wellenformen
Was kann man mit solchen Daten, sofern sie entsprechend aufbereitet sind,
alles steuern ?
Zunächst einmal alle Arten von Generatoren, auch solche, die keine
periodische Wellenform haben, wie zB. die Pseudomembran (gen.psm).
Dann verschiedene Typen von Rauschen, ganz besonders die durch FM generierten
(fmnoise.peak, fmnoise.band).
Filter, die steuerbar sind (lp, hp, bp, notch).
Und natuerlich Oszillatoren, zB. die physikalischen Modelle (osc.chord,
osc.bar, osc.xbar, .nail, .rod, .ring ...).
Dazu müssen die Steuerdaten, wie gesagt aufbereitet werden. Zum Beispiel
durch hugo ('hardly understandable genuin oscillator),
ein eigener analytischer Osziallator, der aber auch Steuerdaten für
beliebige andere Oszillatoren liefern kann.
Das wird das Hauptthema des nächsten Meisterkurses sein.
|
i1=gelassen.wav |
akueto,
G.R.
(c) Günther Rabl, 2013