ELECTRIC OPRPHEUS ACADEMY
SPILLING THE BEANS #16 TWIXEL

Additive Synthese von Klängen, die sich zeitlich weder in der Amplitude noch im Spektrum verändern, ist im Zeitalter der Fouriertransfomtion kein Thema mehr. Man muss nicht mehr, wie weiland Stockhausen, Dutzende von Sinusgeneratoren bemühen und das Ergebnis zusammenmischen. Man setzt die entsprechenden Samples im Spektrum und transformiert das Ganze in die Zeitebene.
Jedes Sample im Spektrum repräsentiert eine konstante Sinusschwingung in der Zeit. Die Position des Samples bestimmt die Frequenz; seine Amplitude (complexer Radius) die Amplitude; seine Phase den Anfangszustand. Ist der Wert des Samples rein reell (ohne imaginären Anteil), dann ist es ein Cosinus; ist es imaginär (ohne reellen Anteil), dann ist es ein Sinus.
Genaugenommen können wir die Fouriertransformation selber als additive Synthese betrachten. Nur sind es sehr viele Samples, die in der Zeitebene, als nah beieinanderliegende Sinusschwingungen, durch gegenseitige Verstärkung und Auslöschung jeden zeitlichen Verlauf bilden können, der in dem gewählten Ausschnitt möglich ist.

Die Anzahl aller möglichen Frequenzen ist dennoch begrenzt: es sind genausoviele, wie der Transformationsbuffer Samples hat.
Bei einem Buffer von 16k wären es 2^16 = 65536 Frequenzen, davon die Hälfte linksdrehend, die andere Hälfte rechtsdrehend ('positive' und 'negative' Frequenzen). Bei einer Samplerate von 44.1k repräsentiert das Sample Nr. 100 im Spektrum die Frequenz 100*sr/dim = 67.29126Hz; das Sample Nr. 101 die Frequenz 67.96417Hz.
Das Intervall, das sie bilden, ist 1.01, ungefähr 1/6 Halbton.
Man kann darüber streiten, ob ein geschultes Ohr den Unterschied wahrnimmt. (Bei so tiefen Frequenzen eher nicht, würde ich sagen). Definitiv wahrnehmen kann das selbst ein nicht geschultes Ohr, wenn die beiden Frequenzen zusammenwirken. Denn dann bilden sie eine Schwebung, die von der Differenzfrequenz abhängt, in diesem Fall 0.67hz, als ein Puls von 1/0.67 = 1.49 Sekunden (die Bufferlänge in Sekunden).

* * *

Wenn wir raffinierte Frequenzgemische auf diese Weise erzeugen wollen, müssen wir Samplepositionen im Spektrum auf ganze Zahlen runden. Dadurch handeln wir uns aber in vielen Fällen solch unerwünschte Schwebungen ein.
Somit stellt sich die Frage: Kann man Schwingungen erzeugen, deren Frequenzen zwischen der Rasterung liegen ? Und wie sieht so ein Sample aus, das zwischen zwei Samples liegt, betwixt two samples - ein 'twixel' ?

Probieren wir es mit folgendem Ansatz:
Eine Sinusschwingung mit 67.29126Hz kann ich ja auch in der Zeitebene generieren und erhalte im Spektrum richtig das Sample Nr. 100 gesetzt, alle übrigen 0. Desgleichen das Sample Nr. 101 bei 67.96417Hz.
Also generiere ich mir eine Frequenz genau dazwischen, 67.62772Hz und sehe mir ihre Repräsentation im Spektrum an. Das Ergebnis wirkt auf den ersten Blick verblüffend:



Das Sample 100 hat den Wert +1, gleich daneben, das Sample 101 den Wert -1; davor ein kurzer Anstieg, danach, schiefsymmetrisch, ein kurzer Abfall - und zwar im Imaginärteil, nicht im Realteil ! (Die Amplitude, die hier für die Grafik normiert ist, ist übrigens 2/π =0.63662).
So also sieht ein Twixel aus !

Betrachtet man die Zahlenwerte der Nachbarsamples, denn erkennt man folgende Reihe:

(Filterprogrammierern müsste die Reihe bekannt vorkommen: Sie findet sich, in anderer Form, auch in der Impulsantwort einer Hilbert-transformation).
Andere Zwischenpositionen zeigen sich unsymmetrisch, mehr oder weniger in die reelle Ebene gedreht, wobei auch Anstieg und Abfall umso steiler werden, je näher man einer ganzzahligen Sampleposition kommt, die schliesslich wieder zu einem rein reellen, einfachen Sample führt.

Ein Algorithmus dafür ist nicht schwer zu finden. Da die Flanken links und rechts anfangs sehr steil verlaufen (umso steiler, je näher einer ganzzahligen Position), genügen meistens ein paar Samples im Umfeld. Eine solcherart generierte Wellenform ist in der ersten Periode etwas irritiert, stabilisiert sich aber bereits ab der zweiten Periode:


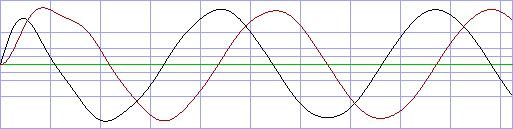
schwarz: Realteil (Cosinus), rot: Imaginärteil (Sinus)

Somit betrachte ich das Twixel als erfunden. (Sorry, falls das schon jemand vor mir entdeckt und anders benannt hat ! - Mir ist nichts dergleichen bekannt).
In VASP ist es jedenfalls ab sofort implementiert als set.twix

* * *

Die Filterprogrammierer sehen es auf einen Blick: So ein Twixel sieht aus wie die typische Impulsantwort eines nicht kausalen Filters (in beide Zeitrichtungen). Was bewirkt es, wenn man es tatsächlich als Impulsantwort eines Filter nimmt ? Ganz einfach: ein Delay in Bruchteilen von Samples, ein Allpass. (Die Phasendrehung lässt sich leicht kompensieren).
Auch das kann nützlich sein, zum Beispiel zum Generieren von Impulsserien mit nicht ganzzahligen Perioden.

prime harmonics

Ein Anwendungsbereich fuer twixel ist die Generierung von Frequenzgemischen, in denen Feinabstufung unbedingt erforderlich ist, zum Beispiel subharmonische Reihen (1 - 1/2 - 1/3 - 1/4 ...) oder logarithmische Frequenzreihen, oder Reihen nach anderen, nichtganzzahligen Charakteristiken.
In VASP gibt es seit kurzem den Generator PH - prime harmonics, mit dem sich Sinusgemische durch Primzahlreihen aufbauen lassen. Bereits die triviale aufsteigende Primzahlreihe 1:2:3:5:7 ... ist interessant, sowohl klanglich, als auch in der Mikrostruktur. Hier die Wellenform eines Frequenzgemisches nach aufsteigenden Primzahlen:


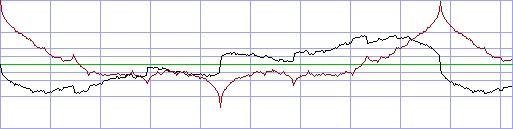
schwarz Realteil, rot Imaginärteil

oder in x/y-Darstellung:



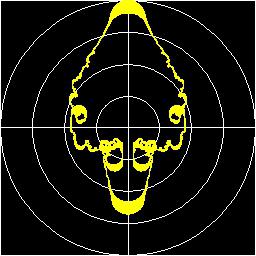
Es liegt auf der Hand, dass solche Wellenformen reizvoll für Parametersteuerungen sein können - seien es Tonhöhenverläufe, oder Raumpositionierungen, oder sonstwas.
Hier das Modell einer Biegeschwingung, dessen Spannung durch die obigen, gegenläufigen Kurven variiert wird:
ph03_biegeschwingung.mp3

Klanglich interessant sind auch die subharmonischen Primzahlreihen selbst:
ph02a.mp3
oder logarithmisch:
ph02b.mp3
oder in einem vorgegebenen Frequenzband:
ph01b.mp3

Damit betreten wir bereits das höchst interessante Gebiet der geometrischen Konstruktion von Klängen. Im Rahmen meiner Studien habe ich mich Anfang der Achzigerjahre ausführlich damit beschäftigt und mit Hilfe eines Messgenerator und Tonband, die verschiedensten Frequenzgemische hergestellt. Es gibt noch Bänder voll Skizzen, Themen und Motiven, aus denen ich gelegentlich etwas mitteilen werde.
Darüber mehr bei nächster Gelegenheit.

akueto
G.R.


--------------------------------------------------------------

Die folgenden scripts funktionieren ab VASP v2.2144 und und AMP v2.958

*----------- ph01
size=18
PH 100,0 (phi=sin); view.; sfstore ph01.wav
PH 100,0 (phi=frac180); view.
PH.sub 2000,0 (amp=lin,phi=sin); bevz 35ms; ovp
sfstore ph01a.wav
PH.range 600,2400,2000 (amp=flat,phi=rand); bevz 35ms; ovp
/vsp (o)
view.
sfstore ph01b.wav
view.

*----------- ph02
size=18
PH.sub 10000,0 (phi=cos,amp=flat); view.
bevz 35ms
ovp
sfstore *a.wav
PH.sub 10000,1 (phi=altcos,amp=flat,freq=log); view.
hk.track 10hz
bevz 35ms
ovp
sfstore *b.wav
PH 40,1 (phi=altcos,amp=sqrt,freq=log); view.
bevz 35ms
ovp
sfstore *c.wav

*------------------ ph03
i1=ph01.wav (s)
k1=colnoise.blue
k2=osc.bar (dim=128,*k1,ini=fix,cyc=2)
k3=osc.bar (dim=128,*k1,ini=fix,cyc=2)
k4=msum (*k2,*k3)
out=*.wav (2:2,*<k2,k3>,opt)
seg=1
dur: 10
k2.tens: 0.25 (c=i1.0,cm=lin,ca=0.1)
k2.elast: 0.001
k2.damp: 10 [damp]
k2.smooth: 3 [damp]
k2.inipos: 0
k2.iniamp: 1
k2.inidur: 0.001
k2.pu: 96
i1.vsp: 1/300
k3.tens: 0.25 (c=i1.1,cm=lin,ca=0.1)
k3.elast: 0.001
k3.damp: 10 [damp]
k3.smooth: 3 [damp]
k3.inipos: 0
k3.iniamp: 1
k3.inidur: 0.001
k3.pu: 96
fo: 0.1