ELECTRIC OPRPHEUS ACADEMY
SPILLING THE BEANS #16 TWIXEL
In the age of the Fourier transform, the additive
synthesis of sounds that neither temporally change in the amplitude, nor
in the spectrum, is not an issue anymore. One no longer has to labor with,
as Stockhausen formerly did, dozens of sine generators and to mix the
end result together. One sets the corresponding samples in the spectrum
and transforms the whole thing in the time domain.
Each sample in the spectrum represents a constant sine vibration in time.
The position of the sample determines the frequency; its amplitude (complex
radius) determines the amplitude, and its phase determines the initial
state. If the value of the sample is purely real (without an imaginary
part), then it is a cosine; if it is imaginary (without a real part),
then it is a sine.
Strictly speaking, we can consider the Fourier transform itself as an
additive synthesis. But there are very many samples that can form each
temporal course in the time domain possible in the chosen excerpt as sine
vibrations lying close to each other through reciprocal amplification
and cancellation.
The number of all possible frequencies is nevertheless limited: There
are exactly as many frequencies as the transformation buffer has samples.
For a buffer of 16 k, it would be 2^16 = 65536 frequencies, half of them
left-turning, the other half right-turning ('positive' and 'negative'
frequencies). At a sample rate of 44.1 k, sample No. 100 in the spectrum
represents the frequency 100*sr/dim = 67.29126 Hz; sample No. 101 represents
the frequency 67.96417 Hz.
The interval they form is 1.01, approximately a 1/6 half tone.
One can argue over whether a trained ear can sense the difference. (At
so many low frequencies rather not, I would say). Even an untrained ear
can definitively sense this if both frequencies concur. Then they form
a beat that is dependent on the difference frequency, in this case 0.67
Hz, as a pulse of 1/0.67 = 1.49 seconds (the buffer length in seconds).
* * *
If we want to create sophisticated frequency mixes in this manner, we
have to round the sample positions in the spectrum into whole numbers.
As a result, we end up in many cases with such undesired beats.
Therefore, the following question arises: Can one create vibrations whose
frequencies lie between the grid? And what does such a sample look like,
one that lies betwixt two samples – a 'twixel' ?
Let's try it with the following approach:
I can also generate a sine vibration of 67.29126 Hz in the time domain
and properly obtain sample No. 100 set in the spectrum with all other
samples set to zero. The same goes for sample No. 101 at 67.96417 Hz.
So I generate a frequency exactly in between, 67.62772 Hz, and take a
look at its representation in the spectrum. At first glance, the result
seems bewildering:

Sample 100 has the value +1, sample 101 right next to it has the value
-1; before it a short ascent, after it, steeply symmetric, a short descent
– and in the imaginary part, not in the real part! (By the way,
the amplitude standardized here for the graph is 2/π
=0.63662).
So this is what a twixel looks like!
When one observes the number values of the neighboring samples, then one
recognizes the following series:
1/9 |
1/7 |
1/5 |
1/3 |
1 |
-1 |
-1/3 |
-1/5 |
-1/7 |
-1/9 |
The series must seem familiar to filter programmers:
It is to be found, in a different form, also in the impulse response of
a Hilbert transform).
Other intermediate positions appear asymmetrical, more or less rotated
in the real domain, whereby the ascent and descent become even steeper
the closer one comes to an integer sample position, which finally leads
to a purely real, simple sample again.
Finding an algorithm for it is not difficult. Since the left and right
flanks run very steep at the beginning (even steeper the closer to an
integer position), most of the time a few samples in the periphery suffice.
One waveform generated in such a way is somewhat irritated in the first
period, but stabilizes itself already from the second period onward:
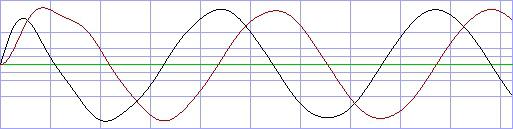
black: real part (cosine), red:
imaginary part (sine)
Therefore, I consider the twixel as invented. (Sorry, in case someone
invented it before me and called it something different! – I am
not aware of anything similar).
In any case, it is implemented in VASP from now on as set.twix.
* * *
The filter programmer spots it at first glance: Such a twixel looks like
the typical impulse response of a non-causal filter (in both time directions).
What does it cause if one actually takes it as the impulse response of
a filter? Very simply: a delay in fractions of samples, an all-pass. (The
phase shift lets itself to be easily compensated).
That can also be useful, for instance, to generate impulse series with
non-integral periods.
prime harmonics
An application field for twixels is the generation of frequency mixes
in which fine tuning is absolutely necessary, for example, sub-harmonic
series (1 - 1/2 - 1/3 - 1/4 ...) or logarithmic frequency series, or series
according to other non-integral characteristics.
Recently added to VASP is the generator PH - prime harmonics,
with which the sine mixture can be built up by prime number series. The
trivially ascending prime number series 1:2:3:5:7 ... is already interesting,
not only soundwise, but also in the microstructure. Here are the waveforms
of a frequency mixture according to ascending prime numbers:
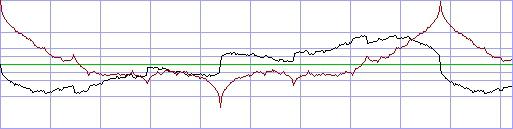
black: real part, red: imaginary part
or in the x/y representation:
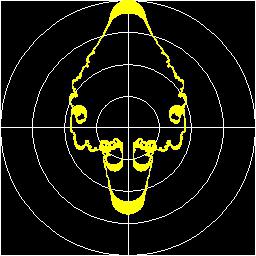
It is obvious that such waveforms could be attractive for parameter controlling
– be they pitch courses or spatial positionings, or whatever else.
Here is the model of a bend vibration whose tension is varied by the upper,
counter-rotating curves:
ph03_biegeschwingung.mp3
Interesting as well from a sound perspective are the sub-harmonic prime
number series themselves:
ph02a.mp3
or logarithmic:
ph02b.mp3
or in a predetermined frequency band:
ph01b.mp3
Therewith we are already entering the highly interesting field of the
geometric construction of sounds. In the scope of my studies I dealt with
it in great detail at the beginning of the 1980s and produced the most
diverse frequency mixtures with the help of a measurement generator and
audiotape. There are still volumes full of sketches, themes and motives
from which I will occasionally disclose something.
More about that at the next opportunity.
akueto
G.R.
*----------- ph01
size=18
PH 100,0 (phi=sin); view.; sfstore ph01.wav
PH 100,0 (phi=frac180); view.
PH.sub 2000,0 (amp=lin,phi=sin); bevz 35ms; ovp
sfstore ph01a.wav
PH.range 600,2400,2000 (amp=flat,phi=rand); bevz 35ms; ovp
/vsp (o)
view.
sfstore ph01b.wav
view.
*----------- ph02
size=18
PH.sub 10000,0 (phi=cos,amp=flat); view.
bevz 35ms
ovp
sfstore *a.wav
PH.sub 10000,1 (phi=altcos,amp=flat,freq=log); view.
hk.track 10hz
bevz 35ms
ovp
sfstore *b.wav
PH 40,1 (phi=altcos,amp=sqrt,freq=log); view.
bevz 35ms
ovp
sfstore *c.wav
*------------------ ph03
i1=ph01.wav (s)
k1=colnoise.blue
k2=osc.bar (dim=128,*k1,ini=fix,cyc=2)
k3=osc.bar (dim=128,*k1,ini=fix,cyc=2)
k4=msum (*k2,*k3)
out=*.wav (2:2,*<k2,k3>,opt)
seg=1
dur: 10
k2.tens: 0.25 (c=i1.0,cm=lin,ca=0.1)
k2.elast: 0.001
k2.damp: 10 [damp]
k2.smooth: 3 [damp]
k2.inipos: 0
k2.iniamp: 1
k2.inidur: 0.001
k2.pu: 96
i1.vsp: 1/300
k3.tens: 0.25 (c=i1.1,cm=lin,ca=0.1)
k3.elast: 0.001
k3.damp: 10 [damp]
k3.smooth: 3 [damp]
k3.inipos: 0
k3.iniamp: 1
k3.inidur: 0.001
k3.pu: 96
fo: 0.1
