ELECTRIC OPRPHEUS ACADEMY
SPILLING THE BEANS #2 CURLY
What is meant by 'prepared piano' is, as I take it, already known: various
objects are fastened onto the piano strings in order to change the character
of sound (pieces of wood, rubber, screws, foils...). In the New Music
of the Twentieth Century it occasionally was the rage and, as a method
of experimental music, is also indispensible today.
A systematic examination of the spectral changes through preparation has,
as far as I know, hardly taken place yet. This can have the very simple
reason that at higher piano notes there are always two or three stings
lying close to each other, and other effects are thus paramount (coupling,
multiple sounds, damping, resonances ...). It can be more clearly studied
on guitar, cello, contrabass or harp - briefly said, on the monochord.
I dealt extensively with it at the end of the Seventies and also found
an approach formula for the change of the partial tones. With its help,
I composed two chamber music-like tape pieces, TRIO I (1979) and TRIO
II (1982), of which only the first was realized, released on WERKE 3 (ccr
403).
Back then, the second trio could not be successfully realized, because
the selected sound type, in which the major triad in the partial tone
series morphed into a minor triad, was almost not able to be produced
and sustained when bowing. However, two fragments of this exist. One of
them is contrabass and cello tones, mounted on tape; the other is a later
attempt with my physical model, generated on the computer.
demo02_trio2_cut.mp3
demo02_trio2_gen.mp3
(For me, it had more to do with the sound type than with illusionistic
replication. Each of the two variants has its specific advantages, and
I would neither want to miss them nor mix them up. Much more can be said
about it, especially in regard to an illusion industry that is striving
for an even larger 'perfection'. More about that another time).
The ideal case for such a preparation provides
that one fastens a weight on a particular position of the string, whereby
the weight should be as punctiform as possible, should not damp and should
not rattle. The effects for each separate partial tone of the string vibration
can be roughly described in the following:
Partial tones that have a vibration node (a flageolet position) at the
position of the weight will not be changed; all others will be lowered
in their frequencies, namely, the more their vibration must move the weight.
Partial tones that have a maximum at the position of the weight will consequently
be lowered the most. Because the change continuously depends on the size
of the weight, 'inharmonic' sounds can systematically be achieved.
So far, so good. But does a piano allow itself to be prepared if one only
has a single recording of it? - Naturally not!
So, after all:
The implicated change of the frequencies of the partial tones can also
be applied to the whole spectrum.
One can imagine it this way: One chooses a 'string' for the preparation
(i.e., the base frequency), a position of the preparation and a relative
weight (in relation to the 'string weight'). However, one does not apply
the scheme of the frequency changes to the overtones of this string, but
rather to all the frequencies of the spectrum.
If one illustrates the changes in a diagram, as a characteristic line,
then the result, depending on the parameters, is a more or less distinct
wavy line: curly.
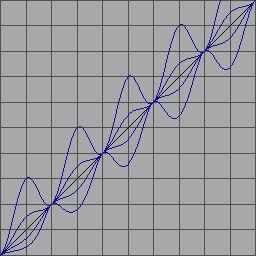
The diagram shows two settings (the wavy lines
downwards) as well as their inversions (upwards). What is amazing about
it - and this also holds true for the physically prepared strings - is
that the alignment of the partial tones (frequencies) can reverse itself.
A higher partial tone can sink lower in its frequency than the adjacent
lower ones. What results is an extreme form of warping (non-linear changes
of the spectrum), which not only has strong impacts on the frequencies,
but also on the temporal structure of the sound. Like all such non-linear
spectral changes, they show their 'pure' form only in the granular application.
a144a_curly.mp3
A brief motif from C. Teuscher (today1), in which 880 Hz is taken as the
base frequency and a weight of 0.3 (30% of the ideal string) at the position
0.2 (measured against the ideal string length 1.0).
In the AMP script it looks like this:
i1=today1.wav (s)
k1=spec.curly (s,*i1,dim=4000)
out=a144a_curly.wav (2:2,*k1)
seg=1
dur: 21
k1.center: 880
k1.relpos: 0.2
k1.weight: 0.3
Such spectral warpings are also in VASP, whereby one must consider that the application in a holistic spectrum (non-granular) also entails strong time phenomena (a type of glissando), which can, however, be quite appealing.
sfload today1.wav
FFT
xwarp.curly 880hz,0.2,0.3
FFT-
play
For the sake of completeness, it is to be said that in both cases an
inverse function of this 'preparation' will actually be applied, which,
however, exhibits a similar character. With a negative parameter for the
relative weight, the original function can be approached.
akueto
G.R.
(c) Günther
Rabl 2010
