ELECTRIC OPRPHEUS ACADEMY
SPILLING THE BEANS #6 THE SOUND OF THE
FOREST
Motto 1:
As one calls into the forest, so does it sound outwards.
Motto 2:
Theoretically speaking, the terms 'theory' and 'practice'
are exactly defined and different from one another. In practice, they
are frequently interchangeable.
During our workshop (from August 28 to September 3, 2010), the idea was
swirling around the room from the first day on to record the sound of
the forest clearing in a way that it could be available as an 'impulse
response' for any desired reverberation.
The weather did not play along; wind and rain thwarted such an undertaking.
First on the final evening, as everything had already been taken down
and the workshop was slowly ending, there was a favorable moment which
Wolfgang Musil used to assemble an appropriate test set-up.

The procedure goes as follows:
One generates a 'sweep' – a sine wave which begins as low as possible
and reaches a high enough frequency within a certain timeframe. (In this
case, within 20 seconds from around 38 Hz to 19 kHz).
This sweep will be played as strongly as possible through a well-placed
loudspeaker, while one or several microphones (beside and behind) record
the resulting spatial sound
So far, so good. The only thing was that we did not
want the sound of the sweep in the forest clearing, but a pure spatial
sound by itself.
The method with which the impulse response from both given sounds (the
original sweep and the recording on site) can be, so to speak, distilled
is called 'correlation'.
In principle, it is a procedure that has already been known for decades
in communications engineering, in order to separate the message information
from the contaminated background noises. (I remember a photo of a monstrous
apparatus with loops of tape and rotating recording heads with which something
like this could, to a certain extent, also be contrived analogously ...).
That is relatively
simple in VASP: One makes a convolution of the one sound with the time
reversal of the other. (Convolution is, as we know, a modulation of the
spectrums). Finished – or almost finished.
A:
sfload original_sweep.wav
mirr
FFT
B:
sfload raumaufnahme.wav
FFT
vmul
FFT-
The result looks like this:

All the way to the left, we actually have the
graphically less conspicuous impulse response of the spatial situation.
All the way to the right, however, we still see quite some mirrored material.
When listening to it, it turns out to be a type of 'synopsis' of the sweep
followed by several echoes. That could be the distortions of the loudspeaker,
which now appear as a 'pre-echo'. (In such processes, the buffer is to
be understood as cyclical).
How ever that came about, there cannot be a pre-echo, so get rid of it
and put an envelope over it right away that definitively ends the sound
at 5.5 seconds, because the rest is noise:

What actually results is a sound type that one can
evoke through an impulse, for instance, by smashing two boards together
– as Michael Zacherl had recently demonstrated. What cannot be overheard
is the portion of the original sweep that is still contained in it.
How does that come about? Our assumption is this: In the open area there
always are air movements, a background noise is always present. The correlation
(even if it is formally and mathematically solved in a completely different
way) basically compares each moment of the one sound with each moment
of the other and finds out to what extent the one sound is contained in
the other, whereby it allows itself to be eliminated from the other. Possibly
the original sweep finds itself again in the diffused background noise-
No problem.
A few months ago I was once again dealing with digital filters and developed
a type of filter which allows amazingly good, precise and controllable
filtering to be carried out (ceir - 'complex exponential impulse response'
– more about that another time).
There is also a variable notch filter which allows individual frequencies
to be suppressed specifically and with adjustable steepness. (The filter
type has already been implemented in VASP and in AMP, but has not been
honed yet, and, therefore, remains to be documented). In any case, one
can trace the course of the sweep with the notch filter and thus largely
eliminate any vestiges of it.
We could be satisfied with it. The end result sounds reasonable, and
it creates a beautiful space in the application as a reverb function.
* * *
But is it really the 'eigensound' of the forest – at least from
one position??

We have no comparison, because we do not have this eigensound itself.
We gain it only through such or similar methods. But one can examine the
method.
* * *
I generate a simple model of a spatial sound through white noise, overlaid
by an envelope (attack-decay) that rises 1.5 seconds and fades 3.5 seconds.
Then I generate the said sweep in a second buffer and 'reverb' both of
them by means of convolution:
A:
load.noise
shape.attdec 1.5sec,3.5sec
FFT
B:
gen.sweep 38hz,19000hz,20sec
FFT
vmul
FFT-
By applying the correlation method, the original, this time synthetic spatial sound would have to come out again now. The VASP script above continues:
(B:)
FFT
A:
load.sweep 38hz,19000hz,20sec
mirr
FFT
vmul
FFT-
How so? – A glance at the spectrums shows it. Sure, we have used an exponentially rising sweep. That also appeared to me as plausible at first sight. The frequency change races through the same intervals at the same times. However, that means that the spectral density continuously decreases upwards and a frequency response, as with pink noise, develops, with a high frequency roll-off of 3dB/octave! This is the spectrum of the sweep:
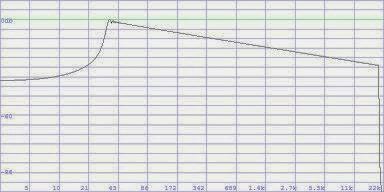
So, another frequency response correction at the appropriate position.
If the frequency response that we created is pink (3dB high frequency
roll-off per octave), then the appropriate correction is 'blue' (3dB high
frequency boost).
In VASP there are these standards as noise (nois.pink, noise.blue), as
well as filters (eir.pink, eir.blue) and as spectral envelopes (env.pink,
env.blue ....).
Here is the whole process with correction:
A:
sfload original_sweep.wav "load
the original sweep in A"
mirr "time mirroring"
FFT "Fourier transformation"
B:
sfload raumaufnahme.wav "load the space recording in
B"
FFT "Fourier transformation"
vmul "spectral multiplication"
env.blue "frequency response correction"
FFT- "inverse transformation"
shape.fall 5.5sec "limited envelope"
opt "optimal level"
(Now one clearly hears the chirping of the crickets,
which had no respect for our recording ...).
Important: The buffer size must be chosen
to be so large that each of the two sounds only fills half a buffer at
the most. Otherwise, convoluted mirrorings in time develop, which cannot
be separated.
(In this case, size=21, approx. 48 seconds in
total).
If one listens exactly, or the sound transposes, then one still notices
modulations with the sweep, particularly at the beginning. I do not know
how this can be completely eliminated during a field recording. Nonetheless,
I viewed our recording process with subsequent correlations as a successful
experiment to close in on sounds that slumber, so to speak, in the landscape
and in the buildings. They are countless; at every position in the space
different!
Naturally, they can be used trivially for 'convolution reverb'.
However, we can just as well view them as individual types of sound and
compose with them. A piece only with spatial sounds! The notion alone
already makes me sit up and take notice ...
* * *
Our process is good enough for collecting material. Material does not
have to be perfect. But some of it can perhaps be improved or simplified.
The frequency response correction is certainly a weak point. That can
already be possibly avoided to some extent.
A suggestion would be a linear sweep, instead
of an exponential one. That probably sounds less impressive, but the frequency
response would also be linear as a consequence.
A second possibility would be to incorporate an amplitude correction right
away in the exponential sweep, so that the tone proportionally becomes
louder upwards. (However, this is a stress test for the loudspeaker).
In order to be able to further experiment, I
have implemented the functions, which were already contained in VASP in
another manner, somewhat more comfortably:
gen.sweep.exp
gen.sweep.lin
gen.sweep.expcorr
sweepnotch.exp
sweepnotch.lin
An exponential sweep (3 arguments: start frequency,
target frequency and duration), one linear, one exponential with level
correction, as well as the associated notch filters for the exponential
and for the linear sweep.
The ideal situation, to stimulate the spatial sound with a 'Dirac impulse'
in which all frequencies are equally contained, is beautiful theory. Even
if one produces it and can transfer it to the air, it would have to be
extremely strong. Even a pistol shot presumably has too much of an individual
sound character. Nonetheless, one should keep this method in view. With
a mechanical device that can more or less reliably produce always the
same, loud impulse (bang), one can record spatial sounds everywhere with
a portable recorder. Especially in larger space situations where the initial
reflection first arrives after a few milliseconds, the triggered bang
can easily be separated from the impulse response. This could suffice
to collect material.
Upcoming are a few considerations about how one could apply such a gained
spatial sound in real-time.
akueto
G.R.
(c) Günther
Rabl 2010
Addendum:
I have also looked up how others do that. By the way, "do" is
good! – Formulas, formulas, formulas ...
(Two pages of formulas can be written about even such a simple thing as
a linear sweep).
That naturally scares people away who do not have a knack for mathematics
– and it can only annoy all others to have to stumble over variants
of the same integral again and again.
There has to be a type of typographical dress code here: The integral
sign is the tie of scientific earnestness.
And are the formulas even correct at all?? ...
Strangely enough, the process, as we have performed
it, is described in several papers as 'autocorrelation'. However, autocorrelation
is the convolution (reverberation, if one likes) of a sound with its own
time reversal. But we are dealing with two different sounds, one of which
is merely somehow contained in the other. Correlation is enough.
The problematic nature of the frequency response of an exponential sweep
is known. Of course, half of all papers call the sweep 'logarithmic',
actually the complete opposite.
[This unending quis pro quo of 'exponential' and 'logarithmic'
can drive me to desperation! It implies that one once learned sometime
that hearing perception is 'logarithmic' according to its nature. Naturally,
it is also only half the truth, but it opines that pitch rows have to
be exponential so that we feel them as linear, which is why such rows
or progressions are then called logarithmic (?). Wherever the mix-up is
to be feared, I rather prefer to use the description 'proportional', such
as, e.g., when controlling the parameters in AMP].
The problem of a linear sweep is also known. (It
passes through the same frequency intervals, not pitch intervals, at the
same times). Its frequency response would be perfectly linear, but the
lower frequencies would pass through so quickly that they could, under
circumstances, no longer stimulate the space properly. That must have
already been tried out.
Also the suggestion of an amplitude correction of the exponential sweeps
is to be found. Has anyone already tried that out? It could namely be
that the low frequencies, in turn, are so faint that they likewise cannot
stimulate the space.
In practice, namely.
The pre-echoes will actually be blamed for the distortions in the transmission
path. But does that also hold true for distortions of odd-numbered order?
(In my opinion, no).
All of that and more has to simply be tried
out – in a model case as in the application. Practice already begins
where theory still has not stopped. (See Motto 2 above).
